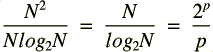
La FFT bidimensionnelle

La FFT (Fast Fourier Transform ou Transformée de Fourier Rapide) est le nom donné aux algorithmes réalisant le calcul de la transformée de Fourier discrète (DFT en anglais) de manière optimisée. Les algorithmes de FFT réalisent généralement un nombre d'opérations (multiplications complexes et additions) de l'ordre de N*log₂(N), où N est le nombre de points sur lesquels le calcul est effectué, alors que la DFT simple en demande N². En faisant le rapport des 2 :

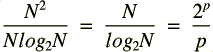
on remarque que sur 256 points, on passe de 65536 à 2048 opérations soit 32 fois moins.

Rappel de l'expression de la DFT :

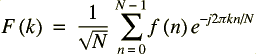
La transformée de Fourier discrète inverse (IDFT) étant :

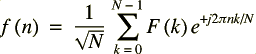
qui s'obtient en conjuguant l'expression de la DFT (on remplace le - par un + dans l'exponentielle) ce qui permet d'utiliser le même code pour réaliser les deux.

La transformée de Fourier discrète bidimensionnelle (2D DFT) est définie par :

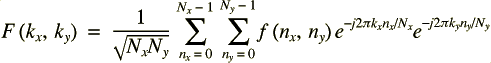
et sa réciproque par :

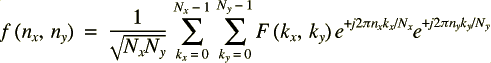
On remarque que l'on peut écrire la 2D DFT ainsi :

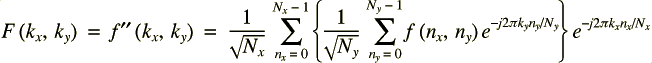
Ou bien encore de la manière suivante :

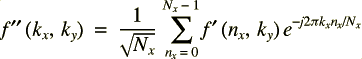
où :

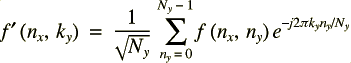
Il suffit donc d'appliquer une DFT sur les colonnes puis sur les lignes, l'ordre n'ayant aucune importance.